In the history of gambling, progressive betting (modifying stakes depending on the previous outcome) was the first and last form of “forcing” an objective strategy to be applicable and effective in casino games governed exclusively by luck, such as roulette. For most players, the move from constant to progressive betting was motivated either by the naive, but so popular, goal of “beating the house” or by a form of safety based on mathematical certainty.
Progressive betting as a gambling system has been analyzed by experts from a strategic and mathematical point of view, including in comparison with constant betting. Among the progressive systems, the one that involves doubling the stake after each loss (the Martingale) has been declared the riskiest. Researchers have revealed links between the use of this progressive system and certain cognitive distortions of gamblers, in particular the so-called ‘Gambler’s fallacy’.
In 1998, researcher Nigel Turner of CAMH (Centre for Addiction and Mental Health, Toronto) conducted a comparative study of the statistical results associated with doubling and constant stakes from the perspective of problem gambling. The conclusions of this study pertained to the interpretation of the results of a computer simulation of the two types of strategies, in the short and long term, and to correlate them with the erroneous conception of many gamblers about random events and the notion of probability.

Progressive betting as a gambling strategy
Progressive betting consists of a series of bets placed over several rounds of the game, the stakes of which are modified from round to round depending on the outcome of the previous round. The most well-known progressive betting systems are the Martingale, the Reverse Martingale, Labouchere, Fibonacci, and D’Alembert. Progressive systems are applicable to bets and games that offer 1 to 1 payout odds (or very close), such as outside bets in roulette – Red/Black, Odd/Even, or Low/High – the game of blackjack or baccarat.
Progressive betting is seen as an objective strategy of playing, and this attribute is supported by the mathematical nature of the principle underlying these systems: No matter how long a series of unfavorable results is, the first win will cancel the accumulated loss and bring profit (Martingale), will cancel the two previous losses (Fibonacci), or will bring profit if the number of won bets becomes equal to the number of lost bets (Labouchere).
However, the final monetary result depends decisively on the player’s bankroll and the betting limits imposed by the casino, because a long succession of losses may deplete the bankroll, or the stake required to complete the system can exceed the casino’s limit. Especially in the case of the Martingale, the loss accumulates exponentially, increasing the risk of bankroll depletion. Thus, progressive systems do not guarantee success, despite their mathematical nature, and, in addition, offer a rather low profit rate. If there were no imposed betting limits and the player had unlimited monetary resources, he would always win with such a system.
Many players use progressive betting systems due to the erroneous assumption that such systems offer them a higher probability of winning than if they were betting with a constant stake, as well as due to a misconception about random events and the laws of probability. Therefore, it is important for problem gambling experts, as well as gamblers themselves, to have a thorough understanding of these systems and their weaknesses.

The first statistical study: Doubling versus constant stake, in reality
The computer simulation was performed using a random number generator in QBASIC, for 1-to-1 bets on an American roulette with the En Prison rule (When the outcome is 0 or 00, the stake is returned to the player, without profit, if the player wins the next bet). The computer runs the program until the player wins, and the loss-win cycle is considered as the length of a playing session, so that all players come to a win under all conditions and regardless of the game strategy. Three independent variables were used, namely the length of the playing session (10, 100, and 1,000 wins), the betting strategy (constant or doubling) and the stake limit imposed by the casino ($100 or $1,000). The initial bet was set at $10 in all cases. The variable whose values were generated was the player’s average net winning at the end of the playing session.
300 simulations were run for each combination hypothesis-variables, for a total of 3,600 simulations. The house edge was 2.63% (due to the En Prison rule), as a compromise between the 1.35% house edge in European roulette with the La Partage and En Prison rules and the 5.26% in American roulette without the En Prison rule. At a different house edge, the average player loss would have been different, but the pattern of results observed would have been the same.
The evaluated variable was described by the statistical indicators mean (M), median (Mdn) and standard deviation (SD):
|
Strategy |
Stake limit |
Indicators |
10 wins |
100 wins |
1,000 wins | ||||||
|
Constant stake |
100 |
M |
-5.5 |
-42.3 |
-560.6 | ||||||
|
Constant stake |
100 |
Mdn |
0.0 |
-35.0 |
-550 | ||||||
|
Constant stake |
100 |
SD |
48.8 |
145.5 |
473.2 | ||||||
|
Constant stake |
1,000 |
M |
-6.2 |
-45.7 |
-556.6 | ||||||
|
Constant stake |
1,000 |
Mdn |
0.0 |
-30.0 |
-570.0 | ||||||
|
Constant stake |
1,000 |
SD |
49.2 |
158.5 |
482.3 | ||||||
|
Doubling stake |
100 |
M |
-12.2 |
-157.2 |
-1,528.37 | ||||||
|
Doubling stake |
100 |
Mdn |
100 |
-110 |
-1,525.0 | ||||||
|
Doubling stake |
100 |
SD |
182.6 |
593.1 |
1,871.2 | ||||||
|
Doubling stake |
1,000 |
M |
16.1 |
-99.5 |
-3,305.7 | ||||||
|
Doubling stake |
1,000 |
Mdn |
100 |
805.0 |
-2,575.0 | ||||||
|
Doubling stake |
1,000 |
SD |
435.6 |
1,752.9 |
6,763.0 |
Results of the simulations in the first statistical study
The net winning distributions for players who bet constantly were largely normal, with a mean slightly below zero. The distributions of outcomes for players who doubled their stakes were slightly negatively deviated, with a mode slightly above zero for short playing sessions and below zero for long playing sessions. In general, doubling the stakes resulted in a higher loss than constant betting. The player is likely to lose much more money if they double their stakes after each loss. The more they play, the more they will lose, and a higher house edge leads to a larger cumulative loss over the long term.
The largest interactive effect found was that of strategy on the number of winning cycles: Over the shortest interval, those who doubled their stakes had an advantage over those who bet constantly ($2.10 vs. -$5.85, respectively). As the number of win-lose cycles increased, doubling their stakes led to a larger cumulative loss than constant betting.
The advantage of those who doubled their stakes over a short period of play is only isolated: After 100 winning bets, at a stake limit of $1,000, the average loss was $99, but the median and mode of the distribution were positive. Thus, most of those who doubled their stakes in just 100 winning cycles will make a profit according to the median and mode, but on average they will lose. Let’s not forget that these results were obtained under the assumption that the player has unlimited bankroll to support the losses.
In the long run, after 1,000 winning cycles and a bet limit of $1,000, the results showed that many players who doubled their stake had net profits, and some of them won around $8,000. However, their losses reached around $30,000. In comparison, the biggest loss of a constant bettor was around $1,900, and the biggest net winning was around $900. Thus, doubling the stake after a loss can increase the chances of winning and potential profit, but in the long run such a strategy leads to a higher average loss.
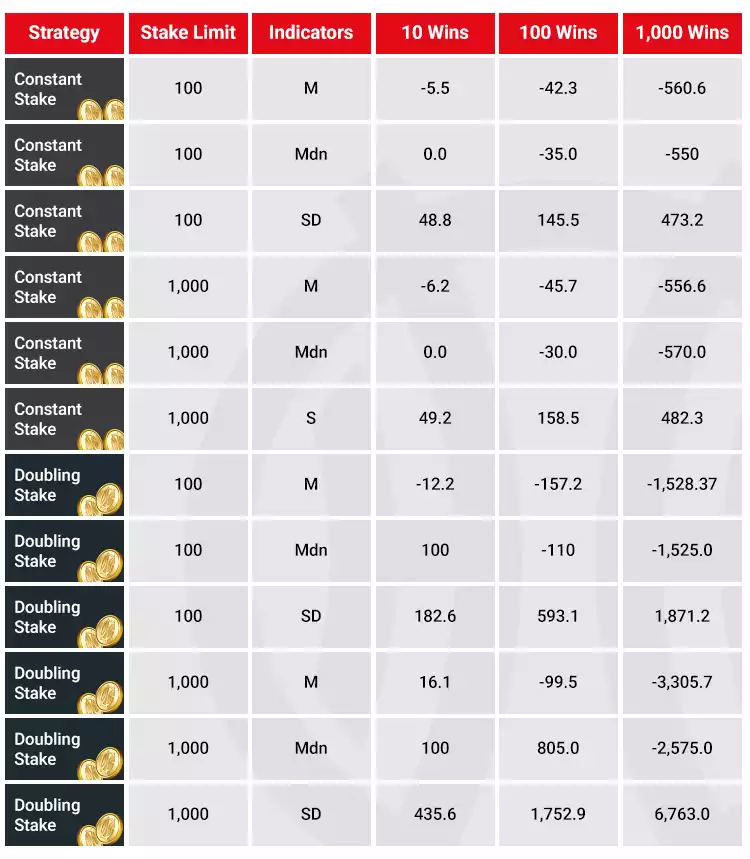
Statistical table comparing constant stake and doubling stake on the first study's simulation
Interpreting the results
The statistical results confirm the general theory according to which as the number of rounds of play increases, the net profit tends to approach the house edge, which is negative, meaning a loss. Doubling the bet, a higher bet limit, and a longer playing period all lead to a greater loss in the long run. In the short run, players who use the doubling strategy are more likely to win than in the long run. However, in the long run, they will lose; this is true even with a high bet limit, because more money is being risked.
Other negative progression systems, without doubling the stake after a loss, but with incremental growth (arithmetic progression), have been tested and compared to the Martingale by experts. When compared to constant betting, all negative progression systems revealed a higher standard deviation of profit, a higher percentage of positive results in the short term, and higher average losses in the long term. The riskier the system (with Martingale at the top), the higher the percentage of players with short-term profit, but with a higher net loss in the long term.
Positive progression systems have also failed the effectiveness test. If the player doubles their stake after winning, they risk their accumulated earnings instead of deepening the debt of their own capital, which at first glance seems like a safe approach, but in terms of long-term averages the result follows the same statistical laws. The principle also applies to incremental positive progression betting systems, which reveal a smaller average loss but much larger than in the case of constant betting at the lower limit.
Psychologists have asked themselves why someone would choose a progressive betting strategy, given the higher risks. It has been suggested that the ups and downs of such a system, especially the Martingale, are seductive, precisely because of the risks. But the dominant principle that would explain this choice is – according to many researchers – that people develop a naive view of randomness and random events, in which the Gambler’s Fallacy is dominant. In this naive view, people create an incomplete or inadequate mental model to represent randomness and the laws of probability.
Illustration of how Martingale System in betting works
The second statistical study: Doubling versus constant stake under (falsely) ideal conditions
Dr. Nigel Turner, in his study, also conducted a second statistical study on the Martingale, to correlate its results with this principle of the naive mental model. The study started from the false hypothesis that the laws of probability are consistent with this mental model and thus the chances of winning increase after a loss, and the chances of losing increase after a win.
The simulation was performed by modifying the original program so that, each time a player wins, the probability of winning the next round is increased by 1/38, and when they lose, the probability is decreased by 1/38. The simulation runs in three strategic situations – betting with a constant stake, doubling the stake and an incremental progression of one unit ($10) after each loss. 100 simulations were run for each situation. The upper limit of the stake was $100, the win/loss cycles were 1,000, and the procedure was the same as in the first statistical study.
Under these conditions, the results showed that the doubling strategy was much more effective than the constant betting strategy (mean M = $3,741, standard deviation SD = 1,366, compared to M = $-290, SD = 374, respectively). The average number of bets before a win was 2.09, almost equal to the number obtained in the first study, in which the real laws of probability were applied.
Conclusions
If the laws of probability followed the false law of “compensation” in the naive mental model of randomness and probability, the doubling strategy or similar systems would be much more effective than constant betting. In reality, the doubling strategy may be more effective only in the short term, under favorable circumstances, which are mainly related to the betting limits imposed by the casino and the player’s own bankroll. This holds true even in live casino games online, where betting limits are strictly enforced to prevent the exploitation of such progressive strategies. In the long term, such a strategy leads to a greater loss than in the case of constant betting. The choice of the doubling strategy is primarily caused by the use of an incomplete or inadequate mental model of randomness and probability.
From the perspective of problem gambling, the study has implications at the theoretical and clinical level. Many gamblers in treatment or counseling have declared that they have considerable gambling skills. Gamblers who double their bets under conditions of high betting limits go home with a profit more often than with a loss, which potentiates the confidence they have in their so-called skills. The results of the statistical study may explain why many “skilled” gamblers enter treatment after suffering very large losses and suggest that it is important for clinicians to understand and use the details of these betting systems in counseling, in order to correct misconceptions and misinterpretations of problem gamblers.
References:
Ethier, S. N. (2010). Betting Systems. In S. N. Ethier (Ed.), The Doctrine of Chances: Probabilistic Aspects of Gambling, 275-316. Springer-Verlag.
Kahneman, D. & Tversky, A. (1982). Judgement under uncertainty: Heuristics and biases. In
Kahneman, D. Slovic, P. & Tversky, A. (Eds). Judgement under uncertainty. Cambridge: Cambridge University Press.
Toneatto, T., & Ladoceur, R. (2003). Treatment of pathological gambling: a critical review of the literature. Psychology of addictive behaviors, 17(4), 284.
Turner, N. E. (1998). Doubling vs. constant bets as strategies for gambling. Journal of Gambling Studies, 14(4), 413-429.
|
About the Author Dr. Cătălin Bărboianu is a mathematician, philosopher, and leading expert in problem gambling research. With a PhD in philosophy, his work spans gaming mathematics, probability theory, and cognitive psychology. A former mathematics educator and associate researcher at the University of Bucharest, Dr. Bărboianu has authored over a dozen books on the mathematics of gambling and contributed to respected journals and platforms including Aeon and American Scientist. His research bridges academic insight with real-world gaming practices, championing responsible gambling and industry transparency. |








